What is the chance Ahok wins the election in one round?
I got a text message earlier today from my brother. He described some statistics from SMRC (a research organisation in Indonesia) about the people's choices for the next Jakarta governor election in 2017. There are 3 candidates for the governor position, one of them is the incumbent, Ahok. Out of 648 people they surveyed, 45.4% choose Ahok, 22.4% for Agus, 20.7% prefer Anies, and 11.5% choose not to disclose or have no choice (link, in Bahasa Indonesia). The question from my brother is, "(if the election is now, when the survey was conducted) what is the chance of Ahok wins the election in one round?" Given that to win the election in one round, Ahok needs to get 50% of the voters.
As I am now practicing my skill on Bayesian probability, I solved this problem using naive Bayesian. An assumption on this problem is that they use random sampling in gathering the samples. In fact, they used multi-stage random sampling, but getting the details of their method is hard, so I think random sampling is a reasonable assumption.
The problem is posed as follows. There are \( n \) samples sampled from \( N \) populations. If \( a \) out of \( n \) choose Ahok, how much the proportion in the population that chooses Ahok? Assuming that \( N \gg n\).
Denote the proportion in the population is \( \eta \), so the probability of the proportion of people choosing Ahok in the population has the value \( \eta \) is
$$ P(\eta | a) = \frac{P(a | \eta) P(\eta)}{P(a)}. $$
\( P(a | \eta) \) denotes the probability of finding \( a \) samples out of \( n \) that chooses Ahok if the proportion in the population is \( \eta\). Due to the population size is much larger than the sample size, we can safely assume that the sampling is sampling with replacement. Thus, from binomial distribution,
$$ P(a | \eta) = \left(\begin{array}{c} n \\ a \end{array}\right) \eta^a (1-\eta)^{n-a}. $$
Now the prior distribution of the value of \( P(\eta) \) is basically just a continuous uniform distribution from 0 to 1, so
$$ P(\eta) = \mathrm{d}\eta\ \mathrm{for}\ \eta\in[0,1]. $$
To find the prior distribution of \( P(a) \), we can integrate \( P(a|\eta) \) for the whole value of \( \eta \) using the prior distribution of \( P(\eta) \). Therefore,
$$ P(a) = \left(\begin{array}{c} n \\ a \end{array}\right) \int_0^1 P(a | \eta)\ \mathrm{d}\eta = \left(\begin{array}{c} n \\ a \end{array}\right) \int_0^1 \eta^a (1-\eta)^{n-a}\ \mathrm{d}\eta. $$
The integral results the Beta function, which is \( P(a) = \left(\begin{array}{c} n \\ a \end{array}\right) B(a+1, n-a+1) \).
Obtaining all the prior distributions, we now can write the distribution of the proportion of the population that choose Ahok known that \( a \) out of \( n \) samples choose Ahok,
$$ P(\eta|a) = \frac{1}{B(a+1, n-a+1)} \eta^a (1-\eta)^{n-a}\ \mathrm{d}\eta. $$
This is known as Beta distribution. For \( n = {10, 20, 50}\) and \( a = n/2\), the probability distribution function (PDF) of the Beta distribution is shown below.
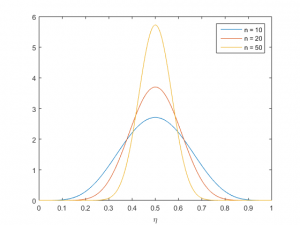
It is seen that as there are more sampling, the variance of \( \eta \) becomes smaller. To get the margin of error with 95% confidence, we can search the range of the distribution to get the area of 0.95, as the area below each plot is integrated to 1. Below is the plot of margin of error with 95% confidence versus number of samples, with \( a/n = 0.5\).
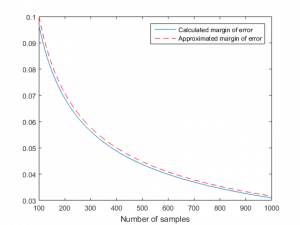
The margin of error with 95% confidence can be approximated by \( \sim 100\%/\sqrt{n}\). This is in agreement with the number the research organisation provided. In their presentation (page 3), they said the respondent is 648 and margin of error about 3.9%, which agrees with our approximated margin of error, \( \sim 100\%/\sqrt{n} \approx 3.93\%\).
Back to the problem. To calculate the probability of Ahok winning the election in one round, he needs \( \eta > 0.5 \). Thus, to calculate the probability, we can integrate the beta distribution from \( \eta = 0.5 \) to 1. It can be achieved by calculating the incomplete beta function.
$$ P(\eta>0.5|a) = \int_{0.5}^1 \frac{\eta^a (1-\eta)^{n-a} d\eta}{B(a+1, n-a+1)}$$
$$ P(\eta>0.5|a) = 1-I(0.5; a+1, n-a+1). $$
Looking at the data, there are 573 respondents that give definite choices. Out of 573 people, 294 people choose Ahok (51.3%) and 48.7% other do not choose Ahok. Thus, \( n=573\) and \( a=294\). Inserting these numbers from the equation above, we obtain
$$ P(\eta>0.5 | a) = 73.5\%. $$
As conclusion, using the random sampling model, we found that the probability of Ahok wins the election in one round (if the election was when the survey was conducted) is 73.5%.