How many papers were submitted to BayesOpt16?
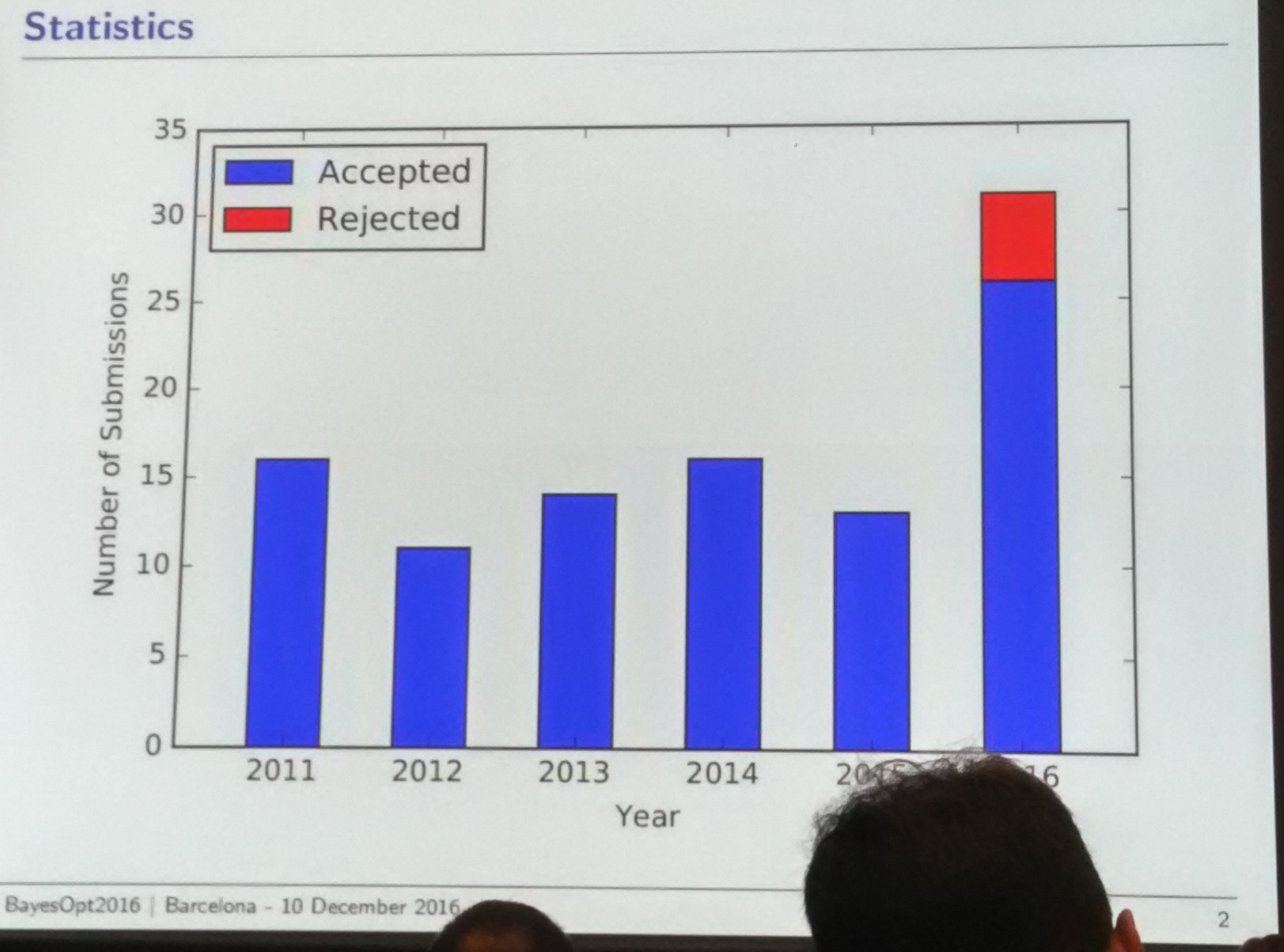
As I mentioned in my recent post, my paper has been accepted for poster presentation at Bayesian Optimisation Workshop at NIPS 2016. List of accepted paper has also appeared on the workshop’s website. There are 26 papers accepted in total. From the submission, my paper was given ID 12 and appears 9th on the list.
Since the list of accepted papers is not ordered in alphabetical order (title nor author), I assume the list is ordered by the submission ID. I also assume that the submission ID is given by the order of submission. The question is “given the above information, estimate how many papers were submitted to BayesOpt 2016?”
Let’s denote \(d=12\) as the \(d\)-th paper submitted, \(r=9\) as the \(r\)-th paper accepted, \(a=26\) as the total accepted papers, and \(s\) as the total papers submitted. It is clear enough to say that \(s \geq a\), as it is impossible to have more accepted papers than submitted papers. Given those information, we want to calculate the probability of \(s\),
\[\begin{equation} P(s|a,d,r) = \frac{P(a|d,r,s)P(s)}{\sum_{s_i=a}^{\infty} P(a|d,r,s_i)P(s_i)}. \label{eq:bayes} \end{equation}\]In order to calculate \(P(a|d,r,s)\) from the equation above, we introduce a new variable, \(\eta\), the acceptance rate for large samples. Given the acceptance rate, \(\eta\), and the total submissions, \(s\), we can calculate the probability of having number of accepted papers, \(a\), using binomial distribution,
\[\begin{equation} \label{eq:a-s-eta} P(a|s,\eta) = \left(\begin{array}{c} s \\ a \end{array}\right) \eta^a (1-\eta)^{s-a}. \end{equation}\]To get the probability distribution value of \(\eta\), we can use beta distribution with information that there are \(r\) papers accepted out of \(d\) submissions. This is in similar form with the result on my previous post,
\[\begin{equation} \label{eq:eta-d-r} P(\eta | d,r)\ \mathrm{d}\eta = \frac{\eta^r (1-\eta)^{d-r}}{B(r+1,d-r+1)}\ \mathrm{d}\eta, \end{equation}\]where \(B(\alpha, \beta)\) is the beta function.
Now we can use equation \eqref{eq:a-s-eta} and \eqref{eq:eta-d-r} to obtain
\[\begin{align} \label{eq:a-d-r-s} P(a|d,r,s) & = \int_0^1 P(a|s,\eta) P(\eta|d,r)\ \mathrm{d}\eta \nonumber \\ & = \left(\begin{array}{c} s \\ a \end{array}\right) \frac{1}{B(r+1,d-r+1)} \int_0^1 \eta^{a+r} (1-\eta)^{s-a+d-r}\ \mathrm{d}\eta \nonumber \\ & = \left(\begin{array}{c} s \\ a \end{array}\right) \frac{B(a+r+1, s-a+d-r+1)}{B(r+1, d-r+1)}. \end{align}\]Obtaining \(P(a|d,r,s)\), we can use the Bayes theorem in equation \eqref{eq:bayes} to estimate the number of submissions. Assuming that the probability of having number of submissions, \(s\), is uniform from \(a\) to \(\infty\). This is also the same prior assumption in German tank problem. As this is a very small number, we can denote it as \(\Omega\). Thus,
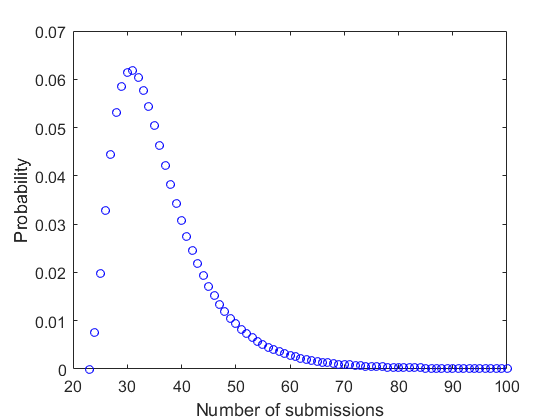
\[\begin{align} \label{eq:final-results} P(s|a,d,r) & = \left(\begin{array}{c} s \\ a \end{array}\right) \frac{B(a+r+1, s-a+d-r+1)}{B(r+1, d-r+1)} \Omega \left[\sum_{s_i=a}^{\infty} \left(\begin{array}{c} s_i \\ a \end{array}\right) \frac{B(a+r+1, s_i-a+d-r+1)}{B(r+1, d-r+1)} \Omega \right]^{-1} \nonumber \\ & = \left(\begin{array}{c} s \\ a \end{array}\right) B(a+r+1, s-a+d-r+1) \left[\sum_{s_i=a}^{\infty} \left(\begin{array}{c} s_i \\ a \end{array}\right) B(a+r+1, s_i-a+d-r+1) \right]^{-1}. \end{align}\]With the equation above, it is now possible to calculate and plot the probability distribution. The probability distribution of number of submissions is shown below.
From the last equation, we can calculate the most probable number of submissions, expected number of submissions as well as its standard deviation. The most probable number of submissions is \(31\), while the expected number of submissions is \(36.5 \pm 9.4\).
UPDATE
In BayesOpt16 workshop, the organiser mentioned that there are 31 papers were submitted to the workshop. The prediction is correct!