Recovering loss information with compressed sensing
One of my favorite fields during my career in academia is compressed sensing. This field feels like a magic to me where one can retrieve 3D information from 2D data and recover 90% loss information of an image as shown below.

When you store an image, you don’t have to store every single bit of information to not distort the image. This is because information in natural images are usually correlated to each other. For example, if I take an image of a scenery and I know the color of a pixel is blue, then the color of the nearby pixels are most likely blue. Thereby, if we lose the information of that pixel, we can still recover its information based on the information of nearby pixel and additional information.

Pixels information in a scenery image are usually correlated.
This knowledge becomes the basis of compression algorithm and compressed sensing. In compression algorithms, the question is how to represent data with as small information as possible without distorting it? In compressed sensing, the question is reversed: how to recover as much information as possible given minimal data?
Let’s explore more about the information correlation in a natural signal. Take the picture above and calculate the absolute difference of a pixel value to the pixel on its right side. The picture will look as below.

Almost all pixels in the picture above are almost zero and only few pixels contain non-zero elements. This is called as sparse, where almost all information are zero and only few of them are non-zero. The original picture can also be said sparse because it can be transformed into sparse representation.
This sparsity property of natural signal is important in compression because it allows us to store only the value and position of the non-zero elements to fully recover the signal. If our storage is very limited, then we can save the most important non-zero elements only by sacrificing the quality of the signal. The more non-zero elements we save, the higher quality of the signal we save.
Let’s play again with sparsity of an image, but instead of taking the absolute difference of neighboring pixels, let’s apply the discrete cosine transform (don’t worry if you don’t know this), take only the \(B\) largest coefficients and transform it back. Here’s an example from my thesis on page 83 where I dropped 90% of the coefficients and took only 10% of the largest coefficients:
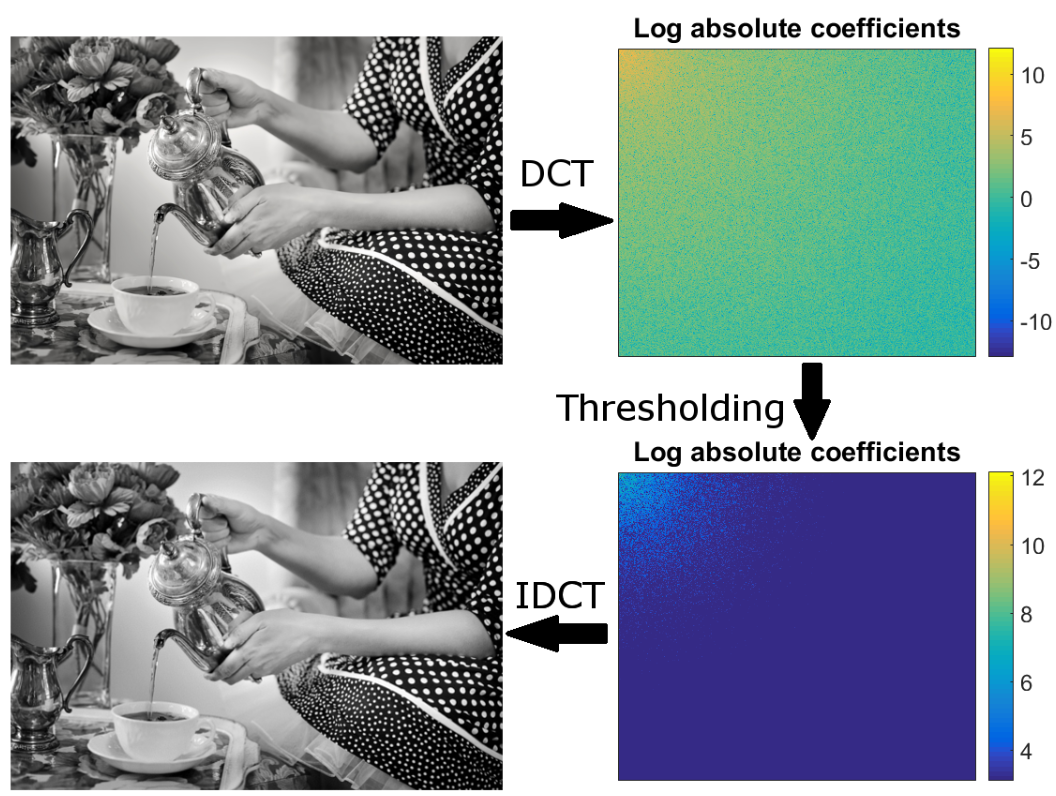
An example where I dropped 90% of the DCT coefficients and recovered an indistinguishable image
It shows that to represent an image, you don’t need all the information, but only a small portion of the image’s information.
A big discovery regarding sparsity was made in 2006 by Candes, Romberg, and Tao (paper). In the paper, they show that it is possible to exactly recover sparse signal of length \(N\) with \(B\) non-zero elements only with \(K\) measurements \((B \ll K \ll N)\). I need to mention that the position of the non-zero elements are unknown before. The same authors also showed that the recovery process is stable even in the presence of noise (paper). This becomes the basis of compressed sensing.
Let’s assume we have an image of size 1280 by 960 pixels (total \(N = 1,228,800\) pixels). As for most natural images, the most important “non-zero” elements of the image would be much less than 1 million. but unfortunately 90% of the pixels are lost (so we only have \(K=122,880\) pixels/measurements). In this case, we can only recover maximum 122,880 non-zero information, but as we see in the picture above, 10% of non-zero values should still be sufficient in recovering an image. Here is a picture, again from my thesis page 88, on recovering 90% of loss information:

(a) The original image. (b) The original image with 90% of information are loss. (c) The retrieved image using compressed sensing.
What does it mean? It means huge: we can retrieve more information than what are measured. One of the most interesting applications is 100 billion frame-per-second camera (paper) where they captured an encoded image (i.e. 2D signal) of a scene, then they recovered a video (i.e. 3D signal) of the scene using compressed sensing. I also invented a three-dimensional spectrometer where one can capture an image as well as the spectrum at each point on the image (paper) and it is based on compressed sensing. A lot more other inventions are based on compressed sensing.